calculating Markoff numbers with matrices

Markoff numbers can be calculated with the aid of particular kinds of continued fractions (see Frobenius for details). However, analogous calculations can be achieved with matrix multiplication, which provides a simpler illustration of the process. So, although I like continued fractions, I will use matrices here.

First, define two matrices, a and b, as follows. Below them are matrices A and B, formed by squaring a and b (respectively).

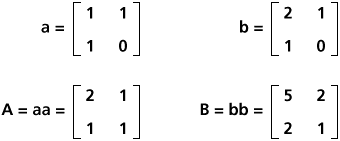
Any Markoff number (except for 1 or 2) can be calculated by taking a particular product of these matrices and examining the upper-left element of the resulting product matrix. For example: 7561 is the upper-left element in the matrix generated as the product bABAABAb. (This kind of notation for the product of a string of matrices is unambiguous, as matrix multiplication is associative.) The bABAABAb matrix is as follows:


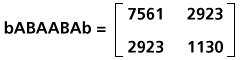
Next to each Markoff number in the tree below is the form of the matrix product (in blue) which generates it:

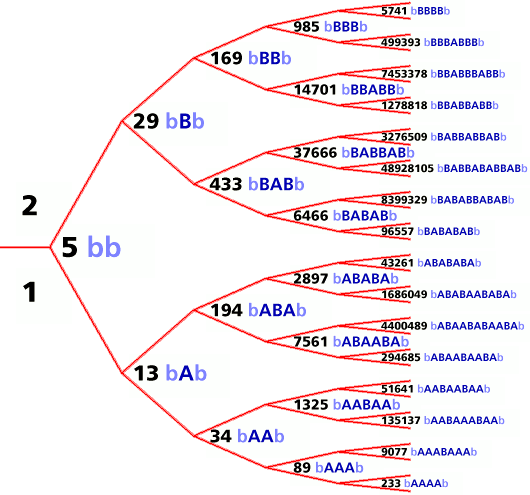
Each matrix product expression (bb, bABAb, etc.) is palindromic. Each expression begins and ends with matrix b; all other terms are A and B matrices. The initial and final b matrices are shown in light blue above; the patterns of A and B terms (in dark blue) are the interesting part. The patterns of A and B terms exhibit the following properties:

• The tree has a complementary symmetry about its center line: the pattern of A and B terms for any number in the tree is the complement of the pattern for the number in the corresponding location in the other half of the tree. E.g, 7561 (ABAABA) and 37666 (BABBAB).
  
  
• The Fibonacci numbers along the bottom edge of the tree have patterns comprised solely of A terms (A, AA, AAA, ...); each pattern has one more A term than its predecessor. The Pell numbers on the other side of the tree have complementary patterns comprised solely of B terms (B, BB, BBB, ...).

• Frobenius describes a method for generating the pattern of A and B terms in these matrix products. I have found a different method; I don't know whether it always gives the same results as the method described by Frobenius, but I have verified that it does for over 200,000 Markoff numbers.
  In this method, the pattern for any other (non-edge) number in the tree is derived from the two (spatially) closest numbers in the preceding level. E.g., for 51461, the two closest numbers in the preceding level of the tree are 1325 and 7561. The new pattern is the shortest possible pattern which starts and ends with the closer of the two preceding patterns, and has the other preceding pattern at its center. E.g., the pattern for 51641 is AABAABAA, which is the shortest possible pattern that starts and ends with AABAA (from 1325, its closer predecessor) and has ABAABA at its center (from 7561, its other predecessor).
  Note: Dr. Serge Perrine informs me that a proof of this conjecture can be found in his book La théorie de Markoff et ses développements.
  
  
• Any other permutation of the A and B terms in the matrix product associated with a Markoff number yields a matrix whose upper-left corner element is higher than the Markoff number. For example, these are the upper-left corner elements associated with the 15 distinct matrix products bXb, where X is comprised of five A and two B matrices:

     bAAAABBb : 7825
     bAAABABb : 7661
     bAABAABb : 7639
     bABAAABb : 7649
     bBAAAABb : 7741
     bAAABBAb : 7729
     bAABABAb : 7571
     bABAABAb : 7561
     bBAAABAb : 7649
     bAABBAAb : 7717
     bABABAAb : 7571
     bBAABAAb : 7639
     bABBAAAb : 7729
     bBABAAAb : 7661
     bBBAAAAb : 7825
  

  Note that smallest value in the list, 7561, is the Markoff number associated with pattern bABAABAb. I have verified this conjecture for over 200 Markoff numbers, including all 127 in the first seven levels of the tree. In every case, the Markoff number was lower than the upper-left corner element of the matrix product of any other permutation of the same number of A and B terms. These verifications can be time-consuming; the patterns quickly grow long, giving many permutations to evaluate. For example, there are 548354040 distinct bXb patterns where X is comprised of 22 A terms and 12 B terms; of those, bABAABAABAABABAABAABAABABAABAABAABAb yields the lowest upper-left corner element in its matrix product: the Markoff number 8976259355318572981.
  Note: Dr. Serge Perrine informs me this conjecture is also easily proven.